Función de distribución de probabilidad
Rango de la función-Valores que toma la variable independiente.
Si en el experimento se tiran dos dados y se suma el valor de sus caras.
La variable aleatoria X sera el espacio muestral
n(s)=36
La variable aleatoria representa la suma de los valores de las caras de los dos dados.
X es el resultado de la suma de los valores
X={2,3,4,5,6,7,8,9,10,12}
Entonces la probabilidad de que la suma sea a ocho ser igual a:
p(X=8)=n(8)/n(s)=5/35
x es el rango, que es igual a la probabilidad de cada un valor de X.
Una variable aleatoria asigna un número real a cada resultad en el espacio muestral.
Una variable aleatoria discreta es aquella con un rango finito.
El evento que esta formado para todos los resultados donde (X=x)
X-Variable aleatoria
x-Valor que toma la variable
Se denota como (X=x) y la probabilidad asociada P{X=x}
f(x)=p(X=x) que va del conjunto de los valores posibles de la variable aleatoria discreta X al intervalo cerrado [0,1] recibe el nombre de función de probabilidad o función de distribución de distribución de probabilidad.
Para una variable aleatoria x satisface las siguientes propiedades
1) f(x)=P(X=x)
2) f(x)≥0 para toda x
3) la sumatoria de f(x)=1
Ejemplo
| Cliente 1 | Cliente 2 | |
| Aprobado | Aprobado | 0.64 |
| Modificar | Aprobado | 0.16 |
| Aprobado | Modificar | 0.16 |
| Modificar | Modificar | 0.04 |
Sea X una variable aleatoria que denota el número de muestras de aire que es necesario analizar para detectar una molécula rara. Suponga que la probabilidad de que una muestra contenga una molécula rara es 0.01 y que las muestras son independientes determine la distrubición de probabilidad de x.
p(muestra contenga una molécula)=0.01
n- no contiene una molécula rara(muestra)
s={s,ns,nns,nnns,nnnns.....}

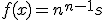
P(s)=0.01
P(s')=1-0.01=0.99


X-1 es el número de muestras que no contienen una molécula rara; n-1.
X Es el numero de muestras inspeccionadas ; n.
p(muestra contenga una molécula)=0.01
n- no contiene una molécula rara(muestra)
s={s,ns,nns,nnns,nnnns.....}

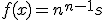
P(s)=0.01
P(s')=1-0.01=0.99


X-1 es el número de muestras que no contienen una molécula rara; n-1.
X Es el numero de muestras inspeccionadas ; n.
Un operador registra el tiempo (redondeado al segundo mas cercano requerido para terminar un ensamble mecánico). Los resultados que obtiene son los siguientes.
segundos (x) 30 31 32 33 34 35 36 37 38 39
número de ensambles 3 5 6 9 12 25 32 15 9 6
X es el tiempo necesario para terminar un ensamble.
a) Determine la función de probabilidad de X
b)Determine la p(33≤x<38) x="x)="n/122" style="text-align: center;">
número de ensambles 3 5 6 9 12 25 32 15 9 6
X es el tiempo necesario para terminar un ensamble.
a) Determine la función de probabilidad de X
b)Determine la p(33≤x<38) x="x)="n/122" style="text-align: center;">

b)P(33≤X<38)=P(X=33)+P(X=34)+P(X=35)+P(X=36)+P(X=37)=0.072+0.098+0.2+0.26+0.12=0.751 P(33≤x<38)=0.751
c)P(X≤35)=0.02+0.04+0.049+0.073+0.018+0.20=0.48 Proporción de ensambles=0.48(122)=58.56 es casi igual a 59
c)P(X≤35)=0.02+0.04+0.049+0.073+0.018+0.20=0.48 Proporción de ensambles=0.48(122)=58.56 es casi igual a 59
Entrada más reciente Entrada antigua Inicio
Suscribirse a:
Enviar comentarios (Atom)


0 comentarios:
Publicar un comentario