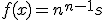Probabilidad..
Vídeo 2 Diagrama de árbol
Vídeo 3 Eventos y subconjuntos
Vídeo 4 Axiomas de probabilidad
Ejercicios para la sección 2-1(Solo nones)...
Proporcione una descripción razonable del espacio muestral de cada uno de los experimentos aleatorios de los ejercicios 2-1 a 2-15. Para cada experimento puede haber más de una interpretación aceptable. Describa todas las hipótesis que plantee.
2-1. Se clasifica cada un de tres partes maquinadas ya sea por encima o por debajo de la especificación establecida para cada una de ellas.
Por encima=PE Por debajo=PD s={(PE,PE,PE),(PE,PE,PD),(PE,PD,PE),(PE,PD,PD),(PD,PE,PE),(PD,PE,PD),(PD,PD,PD), (PD,PD,PE)} n(s)=8
2-3. En la inspección final de fuentes de alimentación electrónicas, pueden presentarse tres tipos de problemas: funcionales, menores, estéticos. Las fuentes defectuosas se clasifican adicionalmente con uno de estos tipos de problemas.
Funcionales=F Menores=M Estéticos=E s={(F),(M),(E),(F,M),(F,E),(M,E),(F,M,E)} n(s)=7
2-5. En la fabricación de una cinta de grabación digital, cada una de las 24 pistas se clasifica de acuerdo con el número de bits erróneos que contiene: ningún bit, o uno o más bits erróneos.
s={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,18,20,21,22,23,24} n(s)=25
2-7. Se utiliza una escala con dos decimales para medir, en toneladas, la cantidad de material que ingresa en una planta química.
x= Al número de toneladas s={x.00,x.01,x.02,x.03,x.04,x.05,x.06,x.07,x.08,x.09,x.10.........x.99} n(s)=100
2-9.Los poros de una varilla de fierro se clasifican como pequeños, medianos o grandes. El número de poros de cada categoría se mide mediante la inspección visual de la muestra.
Poros grandes=G Poros medianos=M Poros pequeños=P s={(G),(M),(P),(G,M),(G,P),(M,P),(G,M,P)} n(s)=7
2-11. La orden de pedido de un automóvil puede especificar transmisión automática o estándar, con o sin aire acondicionado, y uno de cuatro colores: rojos, azul, negro o blanco. Describa el conjunto de todos los pedidos posibles para este experimento.
s={(TA,CA,R),(TA,CA,A),(TA,CA,N),(TA,CA,B),(TA,SA,R),(TA,SA,A),(TA,SA,N),(TA,SA,B),(TE,CA,R),(TE,CA,A),(TE,CA,N),(TE,CA,B),(TE,SA,R),(TE,SA,A),(TE,SA,N),(TE,SA,B)}
n(s)=16
2-13.La orden de compra de un sistema de cómputo puede especificar memoria de 4, 8 o 12 megabytes, y una capacidad de disco duro de 200, 300 o 400 megabytes. Describa el conjunto de todas las posibles órdenes de compra.
s={(4,200),(4,300),(4,400),(8,200),(8,300),(8,400),(12,200),(12,300),(12,400)} n(s)=9
2-15. En un dispositivo de almacenamiento magnético, se hacen tres intentos para leer datos de invocar el procedimiento de recuperación de error, el cual se encarga de volver a posicionar la cabeza de lectura/escritura. El procedimiento de recuperación de error intenta posicionar la cabeza tres veces antes de enviar un mensaje de "operación abortada" al operador. Se definen los siguientes eventos.
s: éxito en la operación de lectura
f: falla en la operación de lectura
F: falla en el procedimiento de recuperación de error
S: éxito en el procedimiento de recuperación de error
A: mensaje de operación abortada enviado al operador
Describa el espacio muestral de este experimento.
.....
2-17 El diagrama de Venn de la figura 2-11 contiene tres eventos. Reproduzca la figura y sombree la región que corresponde a cada uno de los eventos siguientes.
a.A'
b.(A∩B)U(A∩B')
c.(AUB)∩C
d.(BUC)'
e.(A∩B)'UC
Este problema no tenia evento definidos....
2-19. En una operación de modelo por inyección se evalúan varias características de cada parte moldeada.
Sea
A: el evento donde una parte cumple con los requerimientos de ajuste del cliente
B: el evento donde una parte satisface los requerimientos de color del cliente
C: el evento donde cierta longitud crítica cumple con los requerimientos de el cliente
a. Construya un diagrama de Venn que incluya estos eventos, e indique en él la región en la que una parte cumple con todos los requerimientos del cliente. Sombree las áreas que representan los siguientes eventos.
b. B∩C
c.A'UB
d.AUB
e. Si dos de estos eventos fuesen mutuamente excluyentes, cuán exitosa sería esta operación de manufactura?
2-21. Se selecciona una muestra de tres calculadoras de una linea de fabricación y se clasifica cada calculadora como defectuosa o aceptable. Sean A, B y C: eventos en los que, respectivamente, la primera, segunda y tercera calculadora es defectuosa.
a. Describa el espacio muestral de este experimento. Describa cada uno de los siguientes eventos. S={(A,A,A),(A,A,D),(A,D,A),(A,D,D),(D,A,A),(D,A,D),(D,D,A),(D,D,D)}
b.A={(D,A,A),(D,A,D),(D,D,A),(D,D,D)}
c.B={(A,D,A),(A,D,D),(D,D,A),(D,D,D)}
d.A∩B={(D,D,A),(D,D,D)}
e.BUC={(A,A,D),(A,D,A),(A,D,D),(D,A,D),(D,D,A),(D,D,D)}
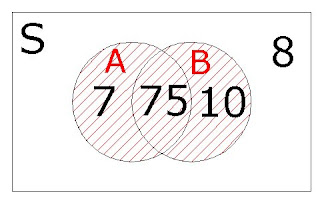
2-23. Se toman muestras de la espuma proporcionada por dos proveedores y se clasifican de acuerdo con la forma en que se adecuan a las especificaciones. A continuación se resumen los resultados obtenidos con 40 muestras.
| | Excelente | Bueno |
| Excelente | 75 | 7 |
| Bueno | 10 | 8 |
Sean
A: el evento donde la muestra tiene un acabado excelente, y B: el evento donde la muestra tiene una longitud excelente. Determine el número de muestras en A'∩B, B', y AUB. Dibuje un diagrama de Venn que represente estos datos.
A={75,7}=82 B={75,10}=85 2-25. Continuación del ejercicio 2-15. Utilice un diagrama de árbol para visualizar el espacio muestral.
2-27. Continuación del ejercicio 2-21. Utilice un diagrama de árbol para visualizar el espacio muestral.
2-29. Cada uno de los cinco posibles resultados de un experimento aleatorio es igualmente probable. El espacio muestral es {a,b,c,d,e,}. Sean
A: el evento {a,b}, y B: el evento {c,d,e}.
Determine lo siguiente.
a. P(A)=2/5
b.P(B)=3/5 c.P(A')=3/5=B
d.P(AUB)={a,b,c,d,e}=1
e.P(A∩B)=0
2-31. Al seleccionar una parte para probarla, la posibilidad de que ésta haya sido producida por una de entre seis herramientas de corte es la misma.
a.Cuál es la probabilidad de que la parte provenga de la herramienta 1?
p=1/6
b.Cuál es la probabilidad de que la parte provenga de las herramientas 3 o 5?
p=2/6
c.Cuál es la probabilidad de que la parte no provenga de la herramienta 4?
p=5/6
2-33. Un espacio muestral contiene 20 eventos igualmente probables. Si la probabilidad del evento A es 0.3, Cuántos resultados contiene el evento A?20(0.3)=6
2-35. El último dígito de una medición de peso puede ser cualquier numero de 0 a 9, todos ellos con la misma probabilidad.
a.Cuál es la probabilidad de que el último sea cero?1/10
b.Cuál es la probabilidad de que último dígito sea mayor o igual que cinco?5/10
2-37. Continuación del ejercicio 2-22. Determine las siguientes probabilidades.
a.p(A)=0.86
b.p(B)=0.89
c.p(A')=1-A=1-.86=0.14
2-39. Continuación del ejercicio 2-23. Determine las siguientes probabilidades.
a.p(A)=0.82
b.p(B)=0.85
c.p(A')=0.18
2-41. Continuación del ejercicio 2-24. Determine las siguientes probabilidades.
a.p(A)=0.5
b.p(B)=0.875
c.p(A')=0.5
2-43. Utilice los axiomas de probabilidad para demostrar los siguiente:
a. Para cualquier evento E, P(E')=1-P(E)
b.p(0)=0
c.Si A está contenido en B, entonces P(A)≤p(B)
2-53.Continuación del ejercicio 2-23. Determine las siguientes probabilidades.
a.p(A)=.82
b.p(B)=.85
c.p(A│B)=75/85=.88
d.p(B│A)=75/82=.91
2-55. Un lote contiene 15 de fierro fundido de un proveedor local y 25 de un proveedor de otro estado. Se eligen dos piezas al azar, sin remplazo, del lote de 40. Sean A: el evento donde la primera pieza seleccionada es del proveedor local, y B: el evento donde la segunda pieza seleccionada es del proveedor local.
a. Cuál es el valor de P(A)?=15/40=0.375
b. Cuál es el valor de P(B│A)?=14/39=.35
c. Cuál es el valor de P(A∩B)?=(0.375)(0.35)=0.13
d. Cuál es el valor de P(AUB)?=0.375+0.35-0.13=0.595
2-57.Continuación de el ejercicio 2-50.
a. Si se sabe que la flecha cumple con los requerimientos de curvatura, Cuál es la probabilidad de que cumpla con los requerimientos de acabado?
b. Si se saqe que la flecha no cumple con los requerimientos de curvatura, Cuál es la probabilidad de que cumpla con los requerimientos de acabo?
2-59 Considere los datos sobre contaminación de obleas y posición electrónica, dados en el ejemplo 2-20. Suponga que de este conjunto se toma al azar una oblea. Sean A: el evento donde la oblea contiene cuatro o más partículas, y B: el evento donde la oblea está en el centro del instrumento de deposición.
a. Cuál es el valor de P(A)?=
b. Cuál es el valor de P(A│B)?
c. Cuál es el valor de P(B)?
d. Cuál es el valor de P(B│A)?
e. Cuál es el valor de P(A∩B)?
f. Cuál es el valor de P(AUB)?
2-61. Un lote de 500 contenedores para jugo de naranja congelado contiene cinco que están defectuosos. Se eligen dos al azar, sin remplazo, del lote.
a. Cuál es la probabilidad de que el primero en ser seleccionado sea defectuoso?
p=4/499
b.Cuál es la probabilidad de que el segundo sea defectuoso dado que el primero es defectuoso?
p=(5/500)(4/499)=0.00008
c.Cuál es la probabilidad de que ambos contenedores sean aceptables?
2-63. Si P(A│B) =1, puede concluirse que A = B? Dibuje un diagrama de Venn para explicar su respuesta.
2-65. Suponga que P(A│B)=0.4 y P(B)=0.5 Calcule lo siguiente
a.P(A∩B)=(0.4)(0.5)=.2
b.P(A'∩B)=(0.6)(0.5)=.3
2-67 La probabilidad de que falle un conector eléctrico que se mantiene seco durante el periodo de garantía, es 1%. Si el conector se humedece, la probabilidad de falla durante el periodo de garantía es 5%. Si el 90% de los conectores se mantienen secos, y el 10% se humedece, qué proporción de conectores fallará durante el periodo de garantía?
P(F)=(0.01)(0.9)+(0.05)(0.1)=0.014
2-69. En la fabricación de un adhesivo químico, el 3% de todos los lotes contienen materia prima que proviene de dos embarques diferentes. Esto sucede cuando los tanques de almacenamiento sea rellenados y lo que queda de un lote es insuficiente para llenar otro tanque.
Sólo es necesario volver a procesar el 5% de los lotes con materia prima que proviene de un solo embarque. Sin embargo, la viscosidad de los lotes que contienen material prima de dos o más embarques es más difícil controlar, y el 40% de estos lotes requieren un procesamiento adicional para alcanzar la viscosidad requerida.
Sean A: l evento en que un lote contiene materia prima de dos embarques diferentes, y B: el evento en que un lote requiere de procesamiento adicional. Determine las probabilidades siguientes.
a.P(A)=3/100=.03
b.P(A')=97/100=.97
c.P(B│A)=40/100=.4
d.P(B│A')=5/100=0.05
e.P(A∩B)=(.03)(0.4)=0.012
f.P(A∩B')=(.03)(0.6)=0.018
g.P(B)=(0.4)(0.03)+(0.05)(0.97)=0.012+0.0485=0.0605
2-71. Las muestras de vidrio de un laboratorio se colocan en empaques pequeños y ligeros o en empaques pesados y grandes. Suponga que el 2% y el 1% de las muestras enviadas en empaques pequeños y grandes, respectivamente, se rompen durante el trayecto a su destino. Si el 60% de las muestras se envían en empaques grandes, y el 40% en empaques pequeños, cuál es la proporción de muestras que se romperán durante el envío?
P(muestras rotas)=(0.02)(0.4)+(0.01)(0.6)=0.008+0.006=0.014
2-73. Continuación del ejercicio 2-60. Utilice la regla de probabilidad total para determinar la probabilidad de que el segundo circuito seleccionado sea defectuoso.
2-77. Si P(A) = 0.2 y P(B) = 0.2, y los eventos A y B son mutuamente excluyentes, puede afirmarse que son independientes?No por que son mutuamente excluyentes.
2-79. Continuación del ejercicio 2-23. Los eventos A y B son independientes?No
2-81. Se toman muestras de espuma de dos proveedores y se hace una evaluación a éstas para determinar el grado con el que cumplen ciertas especificaciones. A continuación se resumen los resultados obtenidos con 126 muestras.
| | sí | no |
| 1 | 80 | 2 |
| 2 | 40 | 2 |
g.P(A)
2-91. Los clientes se encargan de evaluar los diseños preliminares de varios productos. En el pasado, el 95% de los productos que con mayor éxito en el mercado recibieron buenas evaluaciones, el 60% de los productos que con mayor éxito en el mercado recibieron buenas evaluaciones, y el 10% de productos de escaso éxito recibieron buenas evaluaciones. Además, el 40% de los productos ha tenido mucho éxito, el 35% un éxito moderado, y el 25% una baja aceptación.
a. Cuál es la probabilidad de que un producto obtenga una buena evaluación?
b. Si un nuevo diseño obtiene una buena evaluación, cuál es la probabilidad de que se convierta en un producto de gran éxito?
c. Si un producto no obtiene una buena evaluación, cuál es la probabilidad de que se convierta en un producto de gran éxito?
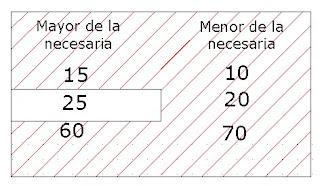
2-93. A continuación se presenta un resumen de la información obtenida de una muestra de 200 partes maquinadas.
| | Mayor de la necesaria | Menor de la necesaria |
| Burda | 15 | 10 |
| Moderada | 25 | 20 |
| Suave | 60 | 70 |
b.Cuál es la probabilidad de que la parte seleccionada tenga una condición moderada en la arista o una profundidad de barrenado menor que la requerida?25+10+20+70/200=0.625
d. Construya un diagrama de Venn que represente los eventos de este espacio muestral.
2-95. Una placa de metaltiene 20 tornillos. Suponga que cinco de ellos no están bien apretados. Se escogen cuatro de ellos, al azar y sin remplazo, para determinar si estan bien apretados.
a. Cuál es la probabilidad de que los cuatro tornillos estén bien apretados?
b. Cuál es la probabilidad de que al menos uno de ellos no esté bien apretado?
2-97. En una operación de llenado automático, la probabilidad de que el volumen de llenado sea incorrecto es 0.001 cuando el proceso se realiza a baja velocidad. Cuando el proceso se efectúa a alta velocidad, la probabilidad de un llenado incorrecto es 0.01. Suponga que el 30% de los contenedores se llena cuando el proceso se efectúa a alta velocidad, mientras que el resto se ejecuta el proceso de lleva a cabo a baja velocidad.
a. Cuál es la probabilidad de encontrar un contenedor lleno con un volumen incorrecto?
b. Si se encuentra un contenedor lleno con un volumen incorrecto, cuál es la probabilidad de que haya sido llenado cuando el proceso se realizaba a alta velocidad?
2-99. Una máquina herramienta está desocupada durante el 15% del tiempo total de uso. Usted le pide al operador que haga uso de la herramienta en cinco ocasiones distintas durante un año. Suponga que las solicitudes de uso son eventos independientes.
a. Cuál es la probabilidad de que la herramienta esté desocupada todas las veces que usted le pide al operador utilizarla?
b. Cuál es la probabilidad de que la herramienta esté desocupada exactamente cuatro de las cinco veces en que usted le pide al operador utilizarla?
c. Cuál es la probabilidad de que la herramienta estédeso cupada al menos tres de las cinco veces en que usted le pide al operador utilizarla?
2-101. Continuación del ejercico 2-100. Se escogen arandelas de un lote al azar u sin remplazo.
a. Cuál es el número mínimo de arandelas que es necesario tomar del lote, para que la probabilidad de que todas ellas sean más delgadas que la dimensión requerida sea menor que 0.10?3
b. Cuál es el número mínimo de arandelas que es necesario tomar del lote, para que la probabilidad de que una o más de ellas sea más gruesas que la dimensión requerida sea al menos 0.90?3
2-103 Continuación del ejercicio 2-102.
a. Cuál es la probabilidad de que en una orden se pida un procesador opcional de alta velocidad teniedo en cuenta que también se solicita memoria adicional?0.78
b. Cuál es la probabilidad de que en una orden se pida memoria adicional teniendo en cuenta que también se solicita un procesador opcional de alta velocidad?0.68
2-105. El circuito siguiente trabaja si, y sólo si, existe una trayectoria de dispositivos en funcionamiento. Suponga que los dispositivos fallan de manera independiente y que la probabilidad de falla de cada uno de ellos es la que se muestra e la figura. Cuál es la probabilidad de que el circuito trabaje?
P(F)=0.02+0.01+0.01+0.01+0.01+0.02=0.08
Retomando el ejemplo 3 de la publicación anterior:
p(Ei│f)= Evento causante de la falla
Alta=0.2
Media=0.3
Baja=0.5
p(f│E1)=0.1
p(f│E2)=0.01
p(f│E3) =0.001
p(E1)=0.2
p(E2)=0.3
p(E3)=0.5
Cual sería la probabilidad de que E1 sea el causante de la falla.
P(E1│f)=p(f│E1)p(E1)/p(pf)=(0.1)(0.2)/0.0235=0.85
Probabilidad de que el producto falle si las condiciones de contaminación es alta?
p(Ek│f)=p(f│Ek)p(Ek)/p(f)
Ejemplo 2:
Suponga que el software para detectar fraude en las tarjetas telefonicas utilizadas por los consumidores registre tpdps los dias el numero de areas metropolitanas donde se originan todos las llamadas.
Se tiene que el 1% de los usuarios legitimos hacen al día llamadas que se originan en 2 o más areas metropolitanas. Sin embargo el 50% de los usuarios fraudulentos hacen al dia llamdas desde dos o más areas metropolitanas la proporcion de usuarios fraudulentos es de 0.01% si el mismo usuario hace en un dia dos o mas llamdas desde dos o mas areas metropolitanas, cual es la probabilidad de que sea fraudulento?
A={Usuario Legitimo}=0.9999
A'={Usuario Fraudulento}=0.0001
p(B│A)=0.01
p(B│A')=0.3
p(A'│B)=p(B│A')p(A')/p(B)
p(A'│B)=p(B│A')p(A')/p(B│A)p(A)+p(B│A')p(A')
p(A'│B)=(0.3)(0.0001)/(0.01)(0.9999)+(0.3)(0.0001)
p(A'│B)=.00003/0.009999+0.00003
p(A'│B)=.00003/0.010029=0.00299
Dos elementos son independientes cuando la probabilidad de uno no influya en la probabilidad de otra.
Son independientes cuando p(A) no influye en probabilidad de p(B)
Regla de la multiplicación:
La probabilidad de p(A∩B) va ser igual a la probabilidad de B por p(AUB)
p(A∩B)=p(B)p(AUB)
Si A y B son dependientes
p(B∩A)=p(A)p(B│A)
Si son independientes
p(A∩B)=p(A)p(B)
p(E1∩E2∩E3∩...∩En)=p(E1)p(E2)p(E3)...p(En)
Ejemplo
Si se selecciona un alumno al azar de un grupo de 200 se sabe que son de tiempo completo (80 mujeres y 60 hombres) y si 60 son de tiempo parcial 40 mujeres y 20 hombres.
Si el evento
A:{El estudiante seleccionado sea de tiempo completo}=140
C:{Que el estudiante seleccionado sea mujer }=120
| | Hombre | Mujer | Total |
| Tiempo completo | 60 | 80 | 140 |
| Tiempo parcial | 20 | 40 | 60 |
| Total | 80 | 120 | 200 |
p(A)=140/200=.7
p(C)=120/200=.6
p(A│C)=p(A∩C)/p(C)=80/120=.66
p(A∩C)=(80/120)(120/200)=80/200=.4
Ejemplo 2:
Proceso de fabricación de semiconductores sea el causante de la falla de el mismo y que .001 expuesto a bajos niveles de contaminación y que la probabilidad de un circuito integrado sea causante de una falla en el producto. En una corrida de producción particular 20% de los circuitos esta expuesto a alto nivel de contaminación, 30% a niveles medios y 50% a bajos niveles. Cual es la probabilidad de que falle un producto que haga uso de uno de esos circuitos?
Altos niveles de contaminación=E1
Niveles medios de contaminación=E2
Bajos niveles de contaminación= E3
p(f)=p(f│E1)p(E1)+p(f│E2)(E2)+p(f│E3)p(E3)
p(f│E1)=0.1
p(f│E2)=0.01
p(f│E3) =0.001
p(E1)=0.2
p(E2)=0.3
p(E3)=0.5
p(f)=(0.1)(0.2)+(0.01)(0.3)+(0.001)(0.5)
p(f)=0.2+0.003+0.0005
p(f)=0.0235
Ejemplo 4:
Probabilidad un conector eléctrico que se mantiene seco durante el periodo de garantía es de 1%, si el conector se humedece la probabilidad de falla durante el periodo de garantía es 5%. Si el 90% de los conectores se mantiene secos y el 10% se humedecen, que proporciones de conectores fallara durante el periodo de garantía.
p(f)=(0.1)(0.9)+(.05)(0.1)
p(f)=0.009+0.005
p(f)=.014
Proporción de elementos que fallan=1.4%
La irregularidad de corte de productos de papel aumenta a medida que las hojas de la cuchilla se desgasta, solo el 1% de los productos cortados con cuchillas nuevas tienen cortes irregulares, el 3% de los cortados con cuchillas de el promedio exhiben irregularidades y el 5% de los cortados con cuchillas desgastadas presentan irregularidades, si el 25% de las cuchillas utilizadas en el proceso de corte son nuevas, el 60% tiene un filo promedio y el 15% están desgastadas.
Cual es la proporción de productos que tendrán cortes irregulares?
Cortes Irregulares = CI
p( CI)=(0.25)(0.01)+(0.6)(0.03)+(0.15)(0.5)
p(CI)=0.0025+0.018+0.0075
p(CI)=0.028
-Al final de el semestre Juan se va a graduar de la facultad de ingeniería Industrial después de tener entrevistas en dos compañías donde quiere trabajar el evaluó la probabilidad que tiene de lograr una oferta de empleo en la compañía A como 0.8 y la probabilidad de obtenerla en la compañía B de 0.6 si por otro lado considera que la probabilidad de que obtendrá una oferta de las dos compañías es 0.5 cual es la probabilidad de que obtendrá una oferta de esas dos compañías.
Probabilidad de que obtendrá al menos una oferta de trabajo de una de esas compañías
P(AUB)=P(A)+P(B)-P(A∩B)= 0.8+0.6-0.5=0.9
-Cual es la probabilidad de obtener un total de 7 u 11 cuando se lanza un par de dados?
Probabilidad de que sume 7={(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}=6/36=1/6
Probabilidad de que sume 11={(5,6),(6,5)}= 2/36=1/18
-Si las probabilidades de que un individuo que compra un automovil de elegir el color verde,blanco,rojo o azul son respectivamente 0.09,0.15,0.21 y 0.23, cual es la probabilidad de que un comprador dado adquiere un automovil nuevo que tenga uno de esos colores.
p=0.09+0.15+0.21+0.23=1
p(s)=1
Los eventos compuestos generan al aplicar las operaciones básicas de los conjuntos a los eventos individuales. Las uniones de eventos, las intersecciones de eventos y los complementos son de interés frecuente. La probabilidad de un evento compuesto a menudo puede obtenerse a partir de las probabilidades de cada uno de los eventos que lo forman. En ocasiones las operaciones básicas de los conjuntos también son útiles para determinar la probabilidad de un evento compuesto.
Ejemplo: La siguiente tabla presenta la historia de 940 obleas de un proceso.
Alta
| no | si | |
| no | 514 | 68 |
| si | 112 | 246 |
Eventos:
A={Altos niveles de contaminación}
B={La oblea está en el centro del instrumento}
a) Como se interpreta AUB y A∩B?
AUB={112,246}
A∩B={246}
b) Calcule la probabilidad de cada evento:
p(A)=358/940=.38
p(B)=314/940=.34
p(AUB)=426/940=.45
p(A∩B)=246/940=.26
La regla de adición:
A∩B=0
p(AUB)=p(A)+P(B)
p(AUB)=p(A)+P(B)-p(A∩B)
Cuando hay tres o mas eventos:
p(AUBUC)=p(A)+p(B)+p(C)-p(A∩B)-p(A∩C)-p(B∩C)+p(A∩B∩C)
Si los eventos son mutuamente excluyentes
p(AUBUC)=p(A)+p(B)+p(C)
(E1∩E2∩E3∩...∩En)=0; P(E1UE2UE3U...UEn)=P(E1)+P(E2)+...P(En)
1) p(s)=1
La probabilidad de un evento siempre estara entre cero y uno.
2) 0≤p(E)≤1
3) Para los eventos E1 y E2 con Ey intersección igual al conjunto vacío.
E1∩E2= 0
p(E1UE2)= p(E1) + p(E2)
p(0) = 0
1.-Los resultados posibles de un experimento aleatorio son
S={a,b,c,d} con probabilidad 0.1, 0.3, 0.5, 0.1.
p(a)=0.1
p(b)= 0.3
p(c)=0.5
p(d)= 0.1
Evento
A={a,b}
B={b,c,d}
C={d}
Encuentre:
p(A)= p(a)+p(b)= 0.1+0.3 = 0.4
p(B)=p(b)+p(c)+p(d)= 0.3+0.5+0.1=0.9
p(C)=p(d)=0.1
p(A')=1-0.4 = 0.6
p(B')=1-0.9=0.1
p(C')=1-0.1=0.9
p(AUB)= p(a)+p(b)+p(c)+p(d)= 0.1+0.3+0.5+0.1= 1
p(A∩B)=p(b)= 0.3
p(A'∩B)=p(d)=0.1
p(B'∩A)=p(a)=0.1
Texto: Probabilidad y estadística para ingenieros
Autor: Douglas C. Montgomery.
Editorial: Mc. Graw Hill
La inspección visual de las obleas de un proceso de fabricación de semiconductores, arrojo los resultados de la siguiente:
| No. De partículas contaminantes | Probabilidad |
| 0 | 0.4 |
| 1 | 0.2 |
| 2 | 0.15 |
| 3 | 0.1 |
| 4 | 0.05 |
| 5 o más | 0.1 |
a) Si se elige una oblea en el proceso, Cual es la probabilidad de que este contaminada?
R= 1-0.4=0.6
b) Cual es la probabilidad de que la oblea tenga tres o mas partículas contaminantes?
R=0.1+0.05+0.1=0.25
c) Cual es la probabilidad de que la oblea contenga cero o mas de 3 partículas contaminantes?
3.- Un fabricante necesita que los diseños de un nuevo producto sean evaluados por clientes en potencial, con la finalidad de obtener comentarios de estos en etapas muy tempranas del diseño. Con base en datos históricos si dos clientes evalúan el producto y deciden de manera independiente, que les gusta, entonces el espacio muestral y las probabilidades pueden modelarse de la siguiente forma.
| Cliente 1 | Cliente 2 | Probabilidad |
| Aprobado | Aprobado | 0.04 |
| Aprobado | Modificar | 0.16 |
| Modificar | Aprobado | 0.16 |
| Modificar | Modificar | 0.64 |
Entradas más recientes Entradas antiguas Inicio