Estadístico:
En una impresora gráfica se utiliza una pieza moldeada antes de firmar un contrato de largo plazo el fabricante de impresora debe asegurarse de que el proveedor puede producir piezas con una desviación estándar de longitud de 0.025mm como máximo para ello se obtiene una muestra aleatoria de 75 piezas obteniendo s=0.022mm. A que conclusión debe llegarse se utiliza una alfa de 0.01.
Parámetro de evaluación-variación en la longitud.
1) H0:σ²≥ (0.025)²
H1:σ²< (0.025)² Valores críticos: 


-1.5<-2.33
Se acepta H0.
Conclusión. Existe evidencia estadística que demuestra que la varianza excede el establecido por tanto no se puede asignar el contrato el proveedor hasta que corrija esta discrepancia.
Estadístico:
ji-cuadrada
Ejemplo:
Un fabricante de detergente liquido esta interesado en la uniformidad de la maquina utilizada para llenar botellas de manera especifica es deseable que la varianza sea; 0.01 onzas² del liquido. Al tomar una muestra aleatoria de 20 botellas se obtiene una varianza muestral (s²) para el volumen de llenado de ese cuadrado s²=0.0153.(distribución normal)
El fabricante esta preocupado por que piensa que la variación del proceso es mayor que la variación histórica. Con un α=0.05, el fabricante tiene elementos que sustenten se preocupación?
1) H0: σ²≤0.01
H1: σ²≤0.01
2) Calcular valores críticos.
3)Decisión.
No hay evidencia estadística para no aceptar H0.
Conclusión: Existe evidencia que la varianza no es mayor al valor histórico por lo tanto, no es necesario hacer ajustes al proceso de llenado.
Existen dos casos:
-Varianzas Iguales(Población)
Estadístico:


-Varianzas Diferentes(Población)
Estadístico:

-Estadístico para la varianza:


Ejemplo:
Se analizan los catalizadores para determinar la forma en que afectan el rendimiento promedio de un proceso químico. De manera especifica el catalizador 1 el que se esta empleando en este momento pero el catalizador 2 también es aceptable. Debido que el catalizador 2 es más económico este puede adaptarse siempre y cuando no cambie el rendimiento del proceso se hace una prueba es una planta piloto los resultados obtenidos aparecen en la siguiente tabla.
| No. de observaciones | Catalizador I | Catalizador II |
| 1 | 91.5 | 89.15 |
| 2 | 94.18 | 90.95 |
| 3 | 92.18 | 90.46 |
| 4 | 95.39 | 93.21 |
| 5 | 91.79 | 97.19 |
| 6 | 89.07 | 97.04 |
| 7 | 94.72 | 91.07 |
| 8 | 89.21 | 92.75 |
| Total | 738.04 | 741.82 |


Existe alguna diferencia entre los rendimientos promedio y cual sería su conclusión.
Parámetro "Rendimiento del proceso"
1)Planteamiento de hipótesis
H0: μ1=μ2
H1: μ1………………=/μ2
2) Calculo los valores críticos para el problema α=0.05

3) Calcule estadístico de prueba t*


-Diferencia de medias (varianza desconocida).

t*=-0.35

Se acepta H0
Conclusión: Existe evidencia estadística que los catalizadores tienen el mismo rendimiento promedio, por tanto podemos usar el catalizador 2 por que es mas económico.
-Si las varianzas son diferentes:
 se debe ajustar en función de los grados de libertad.
se debe ajustar en función de los grados de libertad.

Un fabricante de monitores prueba dos diseños , diseño 1 y diseño 2 para determinar si producen un flujo de corriente satisfactorio.
Fabricante de monitor(Microcircuito).
| Diseño 1 | n1=15 | Media 1=24.2 | Varianza 1=10 |
| Diseño 2 | n2=10 | Media 2=23.9 | Varianza 2=20 |
Con un α=0.1 se desea determinar si existe alguna diferencia significativa en el flujo de corriente promedio donde se supone que las dos poblaciones son normales pero no es posible suponer que las varianzas desconocidas son iguales.
1)Planteamiento
H0: μ1=μ2
H1: μ1………………=/μ2
2)Valores críticos

v=16.6 que es casi igual a 16.

3) Calculo de estadístico:

4) Decisión

Por lo tanto no es posible rechazar H0.
5)Conclusión. Existe evidencia estadística de que los diseños son equivalentes.
Un articulo publicado en una revista científica presenta las siguientes 20 mediciones del tiempo de combustión residual (en segundos) de especímenes tratados de ropa de dormir para niños.
9.85, 9.87, 9.83, 9.85, 9.93, 9.67, 9.62, 9.95, 9.65, 9.94, 9.74, 9.74, 9.93, 9.77, 9.85, 9.99, 9.92, 9.67, 9.75, 9.98, 9.89 .
Se desea encontrar un intervalo de confianza del 95% del tiempo de combustión residual promedio.
a)Encuentre el intervalo de confianza al 95%
b)Si el fabricante tiene al menos un combustión promedio de 9.8 cuenta con los elementos para asegurar ésta conclusión.



a)



b)Tiene una combustión promedio mayor que 9.8

Se acepta H0
Conclusión- No hay evidencia estadística que el compuesto tiene un promedio de consumo mayor a 9.8.
Estadístico:

Un diseñador de productos esta interesado en reducir el tiempo de secado de una pintura tapa poros se prueban dos formulas de pintura.
1.- Contenido químico estándar
2.- Un ingrediente secante que debe reducir el tiempo de secado.
Con la experiencia se sabe que la desviación estándar es igual a 8min y esta variabilidad inherente no debe verse afectada por la adición del nuevo ingrediente .
Se pintan 10 especímenes con la formula 1 y otros con la formula 2, los dos tiempos promedio de secado muestrales son 121min y 112min. respectivamente que conclusiones puede llegar el diseñador del producto sobre la eficacia del nuevo ingrediente utilizando un α=0.05 .
a)Eficacia del nuevo ingrediente:
Ho: μ1≤μ2
H1: μ1>μ2

Conclusión-Existe evidencia estadística de que el nuevo ingrediente reduce el tiempo de secado.
b)Intervalo de confianza

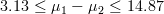
-Para una población:
-Para dos poblaciones:
-Supóngase se desea que el error de la estimación de la conductividad térmica promedio de una cierta clase de hierro con una desviación estándar poblacional de 0.1 sea menor que 0.05 btu/h*ft*°F si queremos un nivel de confianza del 95% encuentre el tamaño de muestra.
Intervalo de confianza para diferencia de medias(varianza conocida)
1 comentarios Publicado por Cristobal Guerrero en 16:59



Criterios:
 - μ1>μ2
- μ1>μ2
 - μ1=μ2
- μ1=μ2
 - μ1<μ2
- μ1<μ2
Ejemplo:
Se lleva acabo las pruebas de la resistencia a la tensión sobre dos diferentes clases de largueros de aluminio utilizados en la fabricación de alas de aeroplanos comerciales de la experiencia pasada con el proceso de fabricación de largueros y del procedimiento de prueba, se supone que las desviaciones estándar de las resistencias a tensión son conocidas. Los datos de la siguiente tabla son resultado de las pruebas hechas.
| | | | |
| | |  |  |
| | | 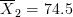 |  |
Si µ1 y µ2 denotan los promedios verdaderos, encuentre el intervalo de confianza del 40% para la diferencia de medias
1- α=
α=1-.9=0.1
0.1/2=0.05


Conclusión: Se escoge el tipo 1, debido que ambos valores son positivos en el intervalo.

Entradas más recientes Entradas antiguas Inicio